Latest revision as of 11:39, 4 August 2014

I received my Ph.D. degree in electrical engineering with a Ph.D. minor in mathematics at the University of Minnesota, Twin Cities Campus in 2012. My Ph.D. studies include research on emerging computing models, reliability of nanoscale circuits, and combinatorics.
Currently I am an assistant professor at Istanbul Technical University (ITU). For up-to-date information please check my group's website at ITU.
Research at the U
As current CMOS-based technology is approaching its anticipated limits, research is shifting to novel forms of nanoscale technologies including molecular-scale self-assembled systems. Unlike conventional CMOS that can be patterned in complex ways with lithography, self-assembled nanoscale systems generally consist of regular structures. Logical functions are achieved with crossbar-type switches. Our model, a network of four- terminal switches, corresponds to this type of switch in a variety of emerging technologies, including nanowire crossbar arrays and magnetic switch-based structures.
Switching Networks
In his seminal Master's Thesis, Claude Shannon made the connection between Boolean algebra and switching circuits. He considered two-terminal switches corresponding to electromagnetic relays. A Boolean function can be implemented in terms of connectivity across a network of switches, often arranged in a series/parallel configuration. We have developed a method for synthesizing Boolean functions with networks of four-terminal switches, arranged in rectangular lattices.
 Shannon's model: two-terminal switches. Each switch is either ON (closed) or OFF (open). A Boolean function is implemented in terms of connectivity across a network of switches, arranged in a series/parallel configuration. This network implements the function  . |
|
 Our model: four-terminal switches. Each switch is either mutually connected to its neighbors (ON) or disconnected (OFF). A Boolean function is implemented in terms of connectivity between the top and bottom plates. This network implements the same function,  . |
Percolation for Robust Computation
We have devised a novel framework for digital computation with lattices of nanoscale switches with high defect rates, based on the mathematical phenomenon of percolation. With random connectivity, percolation gives rise to a sharp non-linearity in the probability of global connectivity as a function of the probability of local connectivity. This phenomenon is exploited to compute Boolean functions robustly, in the presence of defects.
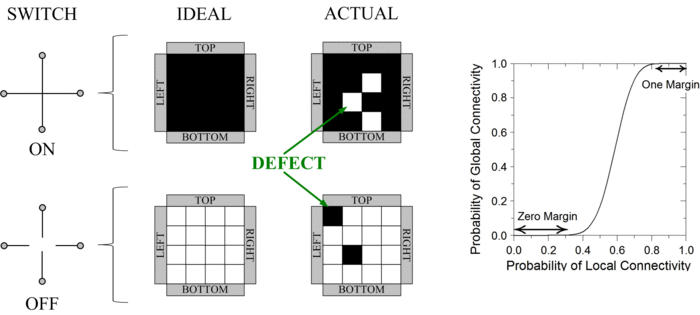
In a switching network with defects, percolation can be exploited to produce robust Boolean functionality. Unless the defect rate exceeds an error margin, with high probability no connection forms between the top and bottom plates for logical zero ("OFF"); with high probability, a connection forms for logical one ("ON").
Contact Information
- Email Address: altu0006@umn.edu
- Cell Phone: 612-978-2955
- Address: 200 Union St. S.E., Room 4-136, Minneapolis, MN 55455





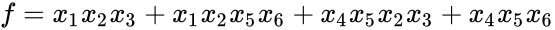 .
.