Revision as of 20:58, 6 August 2011
<sidebar>
- Navigation
- Weikang_Qian|About Weikang
- Research_of_Weikang_Qian|Research
- Publications_of_Weikang_Qian|Publications
- Main_Page|My Advisor's Group
</sidebar>
Most digital circuits are designed to map deterministic inputs of zero and one to deterministic outputs of zero and one. In my research, I consider an alternative paradigm: digital circuits that operate on random Boolean variables. A random Boolean variable with probability p
(0 ≤ p ≤ 1) of being one represents a real-valued number p. Thus, circuits can be viewed as constructs that accept real-valued probabilities as inputs and compute real-valued probabilities as outputs.
I consider three topics pertaining to circuit synthesis in this probabilistic domain. The first is how to synthesize circuits that implement arbitrary arithmetic functions. The second is how to synthesize circuits that transform a set of source probabilities into target probabilities. The third is a special case of the second one, in which the source inputs are independent random Boolean variables with probability 0.5.
The Synthesis of Logical Computation on Random Boolean Variables
Logical computation on random Boolean variables implements a function mapping real values into real values. For example, given an input probability x, an inverter will have an output with probability 1-x. In this work, I consider a general synthesis problem: how can we implement an arbitrary arithmetic function y=f(x) by logical computation on random Boolean variables?
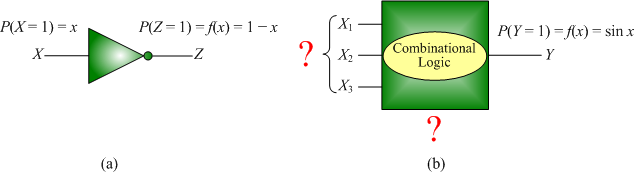
Logical computation on random Boolean variables. (a): Given input probability x, an inverter implements the function f(x)=1-x. (b): A general synthesis problem is how to implement an arbitrary arithmetic function y=f(x) by logical computation on random Boolean variables.
Selected Publications
The Synthesis of Combinational Logic to Generate Probabilities
In probabilistic computation that requires many different probability values, it is expensive to generate all of the probabilities directly from random sources. In this work, I demonstrate novel techniques for synthesizing combinational logic that transforms a set of source
probabilities into different target probabilities.
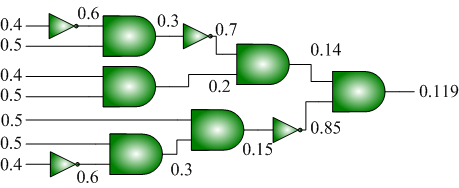
Given a set S of source probabilities {0.4, 0.5}, we can synthesize a combinational circuit to generate an arbitrary decimal output probability. The example shows how to generate 0.119. Each AND gate performs a multiplication of its input probabilities and each inverter performs a one-minus operation of its input probability.
Selected Publications
Two-Level Logic Synthesis for Probabilistic Computation
Assuming that we are given independent copies of probabilistic inputs with probability 0.5 of being one, how can we synthesize a two-level logic circuit that generates an arbitrary target output probability? This problem is equivalent to finding a Boolean function with m minterms and having a sum-of-product expression with the minimum number of products.
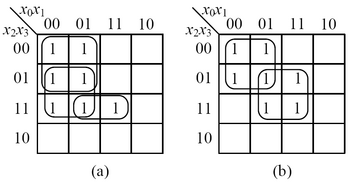
The
Karnaugh maps of two different Boolean functions both containing 7 minterms. (a): The optimal sum-of-product expression contains 3 product terms. (b): The optimal sum-of-product expression contains 2 product terms. Figure (b) gives a Boolean function with the minimum number of products to cover 7 minterms.
Selected Publications




