Research of Weikang Qian

(My research while at UMN.)

Most digital circuits are designed to map deterministic inputs of zero and one to deterministic outputs of zero and one. In my research, I consider an alternative paradigm: digital circuits that operate on random Boolean variables. A random Boolean variable with probability p (0 ≤ p ≤ 1) of being one represents a real-valued number p. Thus, circuits can be viewed as constructs that accept real-valued probabilities as inputs and compute real-valued probabilities as outputs.

I consider three topics pertaining to circuit synthesis in this probabilistic domain. The first is how to synthesize circuits that implement arbitrary arithmetic functions. The second is how to synthesize circuits that transform a set of source probabilities into target probabilities. The third is a special case of the second one, in which the source inputs are independent random Boolean variables with probability 0.5.

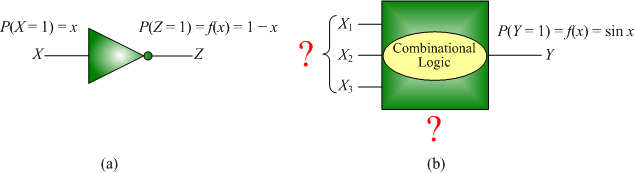
The Synthesis of Logical Computation on Random Boolean Variables

Logical computation on random Boolean variables implements a function mapping real values into real values. For example, given an input probability x, an inverter will have an output with probability 1-x. In this work, I consider a general synthesis problem: how can we implement an arbitrary arithmetic function y=f(x) by logical computation on random Boolean variables?

Logical computation on random Boolean variables. (a): Given input probability x, an inverter implements the function f(x)=1-x. (b): A general synthesis problem is how to implement an arbitrary arithmetic function y=f(x) by logical computation on random Boolean variables.

Selected Publications

title: Synthesizing Logical Computation on Stochastic Bit Streams authors: Weikang Qian and Marc Riedel submitted to: Communications of the ACM Research Highlight.

Paper

title: An Architecture for Fault-Tolerant Computation with Stochastic Logic authors: Weikang Qian, Xin Li, Marc Riedel, Kia Bazargan, and David Lilja appeared in: IEEE Transactions on Computers, vol. 60, no. 1, pp. 93-105, 2011.

Paper

title: The Synthesis of Robust Polynomial Arithmetic with Stochastic Logic authors: Weikang Qian and Marc Riedel presented at: Design Automation Conference, Anaheim, CA, 2008

Paper

Slides

title: Uniform Approximation and Bernstein Polynomials with Coefficients in the Unit Interval authors: Weikang Qian, Marc Riedel, and Ivo Rosenberg appeared in: European Journal of Combinatorics, vol. 32, no. 3, pp. 448-463, 2011.

Paper

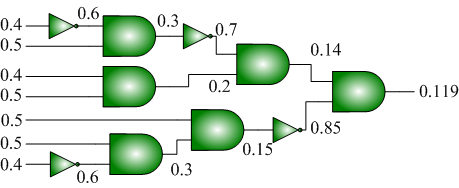
The Synthesis of Combinational Logic to Generate Probabilities

In probabilistic computation that requires many different probability values, it is expensive to generate all of the probabilities directly from random sources. In this work, I demonstrate novel techniques for synthesizing combinational logic that transforms a set of source probabilities into different target probabilities.

Given a set S of source probabilities {0.4, 0.5}, we can synthesize a combinational circuit to generate an arbitrary decimal output probability. The example shows how to generate 0.119. Each AND gate performs a multiplication of its input probabilities and each inverter performs a one-minus operation of its input probability.

Selected Publications

title: Transforming Probabilities with Combinational Logic authors: Weikang Qian, Marc Riedel, Hongchao Zhou, and Jehoshua Bruck will appear in: IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems.

Paper

title: The Synthesis of Combinational Logic to Generate Probabilities authors: Weikang Qian, Marc Riedel, Kia Bazargan, and David Lilja presented at: International Conference on Computer-Aided Design, San Jose, 2009 nominated for IEEE/ACM William J. McCalla ICCAD Best Paper Award

Paper

Slides

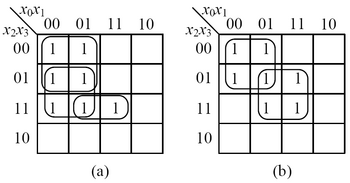
Two-Level Logic Synthesis for Probabilistic Computation

Assuming that we are given independent copies of probabilistic inputs with probability 0.5 of being one, how can we synthesize a two-level logic circuit that generates an arbitrary target output probability? This problem is equivalent to finding a Boolean function with m minterms and having a sum-of-product expression with the minimum number of products.

The Karnaugh maps of two different Boolean functions both containing 7 minterms. (a): The optimal sum-of-product expression contains 3 product terms. (b): The optimal sum-of-product expression contains 2 product terms. Figure (b) gives a Boolean function with the minimum number of products to cover 7 minterms.

Selected Publications

title: Two-Level Logic Synthesis for Probabilistic Computation authors: Weikang Qian and Marc Riedel presented at: International Workshop on Logic and Synthesis, Irvine, CA, 2010

Paper

Poster

title: Synthesizing Cubes to Satisfy a Given Intersection Pattern authors: Weikang Qian and Marc Riedel presented at: International Workshop on Logic and Synthesis, Irvine, CA, 2010

Paper

Slides