Research
"You see things; and you say, 'Why?' But I dream things that never were; and I say, 'Why not?'"
–– George Bernard Shaw (1856 –1950)
Our research spans different disciplines ranging from digital circuit design, to algorithms, to mathematics, to synthetic biology. It tends to be inductive (as opposed to deductive) and conceptual (as opposed to applied). A recurring theme is building systems that compute in novel or unexpected ways with new and emerging technologies.
Storing Data with Molecules
All new ideas pass through three stages:
- It can't be done.
- It probably can be done, but it's not worth doing.
- I knew it was a good idea all along!
––Arthur C. Clarke (1917–2008)
Ever since Watson and Crick first described the molecular structure of DNA, its information-bearing potential has been apparent. With each nucleotide in the sequence drawn from the four-valued alphabet of {A, T , C, G}, a molecule of DNA with n nucleotides stores 2n bits of data.
- Could we store data for our computer systems in DNA? "Can't be done – too hard."
- Is it worth doing? "Definitely not. It will never work as well as our hard drives do."
- But one can store so much data so efficiently! "I knew it was a good idea all along!"
|

|

|
Computing with Molecules
"Biology is the most powerful technology ever created. DNA is software, protein are hardware, cells are factories."
––Arvind Gupta (1953– )
Computing has escaped! It has gone from desktops and data centers into the wild. Embedded microcontrollers – found in our gadgets, our buildings, and even our bodies – are transforming our lives. And yet, there are limits to where silicon can go and where it can compute effectively. It is a foreign object that requires a electrical power source.
We are studying novel types of computing systems that are not foreign, but rather an integral part of their physical and chemical environments: systems that compute directly with molecules. A simple but radical idea: compute with acids and bases. An acidic solution corresponds to a "1" and a basic solution to "0".
|
It's more complex that acids and bases, but DNA is a terrific chassis for computing. We have developed "CS 101" algorithms with DNA: Sorting, Shifting and Searching:
|
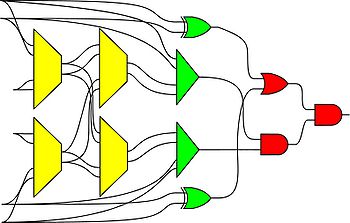
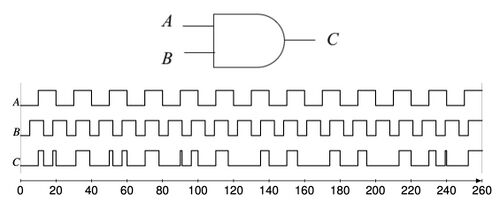
Based on a bistable mechanism for representing bits, we have implemented logic gates such AND, OR, and XOR gates, as well as sequential components such as latches and flip-flops with DNA. Using these components, we have built full-fledged digital circuits such as a binary counters and linear feedback shift registers.
|
Also, we have performed signal processing including operations such as filtering and fast-fourier transforms (FFTs) with DNA.
|
Please see our "Publications" page for more of our papers on these topics.
Computational Immunology
“Physics is the study of the simple things in the Universe. Biology is the study of the complex ones. ”
–– Richard Dawkins (1941– )
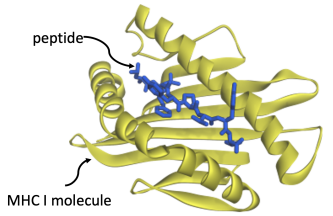
We are studying a problem that computer science currently judges to be very difficult: predicting cellular immunity. It centers on the question of how strongly molecules binds to one another. The molecules in question are peptides – fragments of proteins from a virus – binding to cell-surface receptors. A peptide will only bind if it fits like a key into a lock.
The binding is a critical step in a critical component of the immune system: it allows circulating T-cells to kill off infected cells. If this mechanism succeeds, an infection is stopped in its tracks. If it fails, then infected cells become factories for reproducing copies of the virus; full-blown disease results. Given a novel pathogen, such as SARS-Cov-2, predicting whether the immune system of an individual will do its job at fighting off the disease comes down to predicting how well the viral peptides bind to the cell-surface receptors of that person. We are tackling the problem with cloud computing resources, donated by Oracle:
|
Computing with Random Bit Streams
"To invent, all you need is a pile of junk and a good imagination." –– Thomas A. Edison (1847–1931)
Humans are accustomed to counting in a positional number system – decimal radix. Nearly all computer systems operate on another – binary radix. We are so accustomed to these systems that it counterintuitive to ask: can we compute using a different representation? and why would we want to?
Stochastic Logic
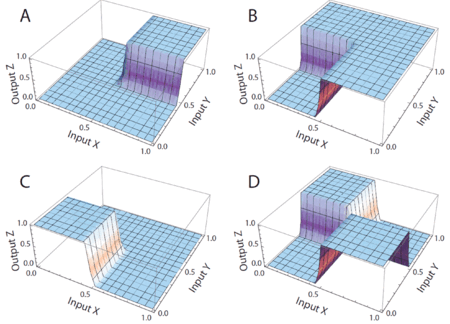
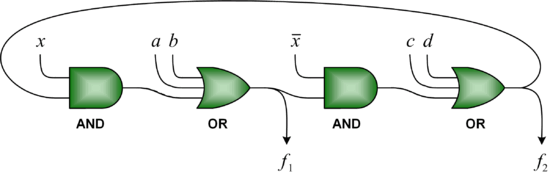
We advocate an alternative representation: computing on random bit streams, where the signal value is encoded by the probability of obtaining a one versus a zero. Why compute this way? Using stochastic logic, we can compute complex functions with very, very simple circuits. For instance, we can perform multiplication with a single AND gate and addition with a single MUX:
Using conventional binary, building a circuit that computes, say a polynomial approximation to a trigonometric function such as tanh(x) or cos(x), requires thousands of logic gates. With stochastic logic, we have shown that we can compute such functions with about a dozen logic gates, so a 100X reduction in gate count. Our most important contribution is a general methodology for synthesizing polynomial functions with stochastic logic, one of the seminal contributions to the field:
|
Logic that Generates Probabilities
We have also shown how to synthesize logic that transforms a set of source probabilities into different target probabilities.
|
A Deterministic Approach
Having championed stochastic logic for many years, we decided to reexamine its foundations. Why can complex functions be computed with such simple circuits when we compute on probabilities? Intuition might suggest that somehow we are harnessing deep aspects of probability theory. This intuition is wrong.
The keys is that we operate on uniform representation rather than a positional one. We showed that we can compute deterministically using the same structures that we use when computing stochastically. There is no need to do anything randomly! This upended the field that we had pioneered.
|
Time-Encoded Computing
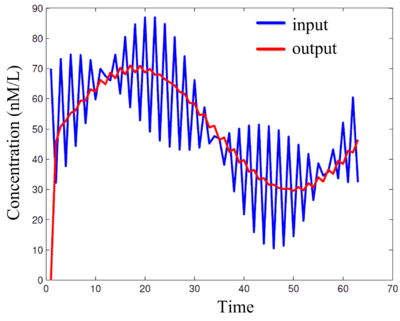
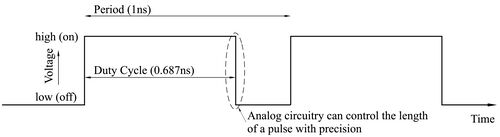
Computing deterministically on bit streams really means that, instead of encoding data in space, we encode them time. The time-encoding consists of periodic signals, with the value encoded as the fraction of the time that the signal is in the high (on) state compared to the low (off) state in each cycle.
As technology has scaled and device sizes have gotten smaller, the supply voltages have dropped while the device speeds have improved. Control of the dynamic range in the voltage domain is limited; however, control of the length of pulses in the time domain can be precise. Encoding data in the time domain can be done more accurately and more efficiently than converting signals into binary radix. So we can compute more precisely, faster, and with fewer logic gates:
|
Please see our "Publications" page for more of our papers on these topics.
Computing with Feedback
"A person with a new idea is a crank until the idea succeeds." –– Mark Twain (1835–1910)
The accepted wisdom is that combinational circuits (i.e., memoryless circuits) must have acyclic (i.e., loop-free or feed-forward) topologies. And yet simple examples suggest that this need not be so. We advocate the design of cyclic combinational circuits (i.e., circuits with loops or feedback paths). We have proposed a methodology for synthesizing such circuits and demonstrated that it produces significant improvements in area and in delay.
|
Please see our Publications page for more of our papers on this topic.
Computing with Nanoscale Lattices
"Listen to the technology; find out what it’s telling you.” –– Carver Mead (1934– )
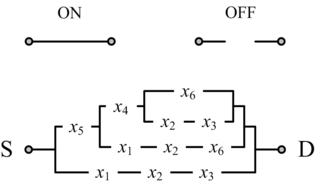
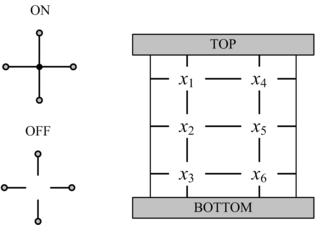
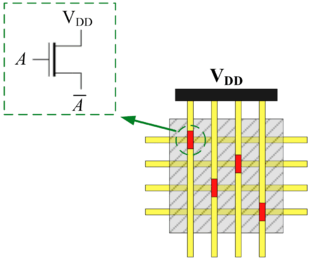
In his seminal Master's Thesis, Claude Shannon made the connection between Boolean algebra and switching circuits. He considered two-terminal switches corresponding to electromagnetic relays. A Boolean function can be implemented in terms of connectivity across a network of switches, often arranged in a series/parallel configuration. We have developed a method for synthesizing Boolean functions with networks of four-terminal switches. Our model is applicable for variety of nanoscale technologies, such as nanowire crossbar arrays, as molecular switch-based structures.
|
The impetus for nanowire-based technology is the potential density, scalability and manufacturability. Many other novel and emerging technologies fit the general model of four-terminal switches. For instance, researchers are investigating spin waves. A common feature of many emerging technologies for switching networks is that they exhibit high defect rates.
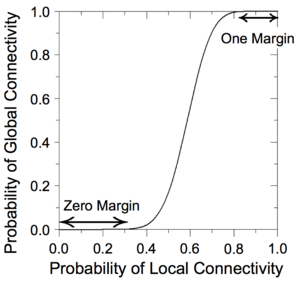
We have devised a novel framework for digital computation with lattices of nanoscale switches with high defect rates, based on the mathematical phenomenon of percolation. With random connectivity, percolation gives rise to a sharp non-linearity in the probability of global connectivity as a function of the probability of local connectivity. We exploit this phenomenon to compute Boolean functions robustly in the presence of defects.
|
Please see our "Publications" page for more of our papers on these topics.
Algorithms and Data Structures
"There are two kinds of people in the world: those who divide the world into two kinds of people, and those who don't." –– Robert Charles Benchley (1889–1945)
Consider the task of designing a digital circuit with 256 inputs. From a mathematical standpoint, such a circuit performs mappings from a space of Boolean input values to Boolean output values. (The number of rows in a truth table for such a function is approximately equal to the number of atoms in the universe – rows versus atoms!) Verifying such a function, let alone designing the corresponding circuit, would seem to be an intractable problem.
Circuit designers have succeeded in their endeavor largely as a result of innovations in the data structures and algorithms used to represent and manipulate Boolean functions. We have developed novel, efficient techniques for synthesizing functional dependencies based on so-called SAT-solving algorithms. We use Craig Interpolation to generate circuits from the corresponding Boolean functions.
|
Please see our "Publications" page for more of our papers on this topic. (Papers on SAT-based circuit verification, that is, not on squids.)
Mathematics
"Mathematics may be defined as the subject in which we never know what we are talking about, nor whether what we are saying is true." –– Bertrand Russell (1872–1970)
The great mathematician John von Neumann articulated the view that research should never meander too far down theoretical paths; it should always be guided by potential applications. This view was not based on concerns about the relevance of his profession; rather, in his judgment, real-world applications give rise to the most interesting problems for mathematicians to tackle. At their core, most of our research contributions are mathematical contributions. The tools of our trade are discrete math, including combinatorics and probability theory.
|
Please see our "Publications" page for more of our papers on this topic.

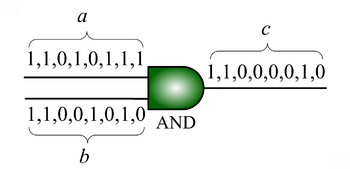
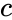 that is the product of the of the input probabilities
that is the product of the of the input probabilities  and
and  .
.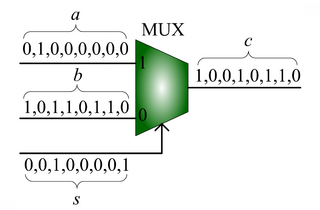
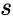 , the MUX produces an output probability
, the MUX produces an output probability 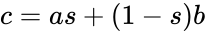 .
.
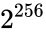 Boolean input values to Boolean output values. (The number of rows in a
Boolean input values to Boolean output values. (The number of rows in a 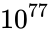 rows versus
rows versus 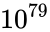 atoms!) Verifying such a function, let alone designing the corresponding circuit, would seem to be an intractable problem.
atoms!) Verifying such a function, let alone designing the corresponding circuit, would seem to be an intractable problem.